Pipelining in TypedProtocols

{-# LANGUAGE BangPatterns             #-}
{-# LANGUAGE FlexibleInstances        #-}
{-# LANGUAGE RankNTypes               #-}
{-# LANGUAGE ScopedTypeVariables      #-}
{-# LANGUAGE StandaloneDeriving       #-}

{-# LANGUAGE DataKinds                #-}
{-# LANGUAGE EmptyCase                #-}
{-# LANGUAGE GADTs                    #-}
{-# LANGUAGE PolyKinds                #-}
{-# LANGUAGE StandaloneKindSignatures #-}
{-# LANGUAGE TypeFamilies             #-}
{-# LANGUAGE TypeOperators            #-}

module TypedProtocolPipelining where

import           Prelude hiding (last)
import           Data.Function ((&))
import           Data.Kind (Type)
import           Data.Void

The typed-protocols is a framework for writing binary session types in Haskell. It has been developed by IOHK in collaboration with Well-Typed.

For network applications it is common to use some form of latency hiding for performance reasons. Network is utilised best when constant pressure is applied to avoid shrinking of the tcp window (e.g. tcp flow control mechanism). Network utilisation is a balance between keeping the most constrained resource busy - but only just - too busy and delay increases and application responsiveness can drop. For these reasons, the typed-protocol package allows to express protocol pipelining. In addition, protocol pipelining should in principle allow to make less context switches and improve data locality.

In this blog post we will study pipelining starting with a simple ping pong protocol:

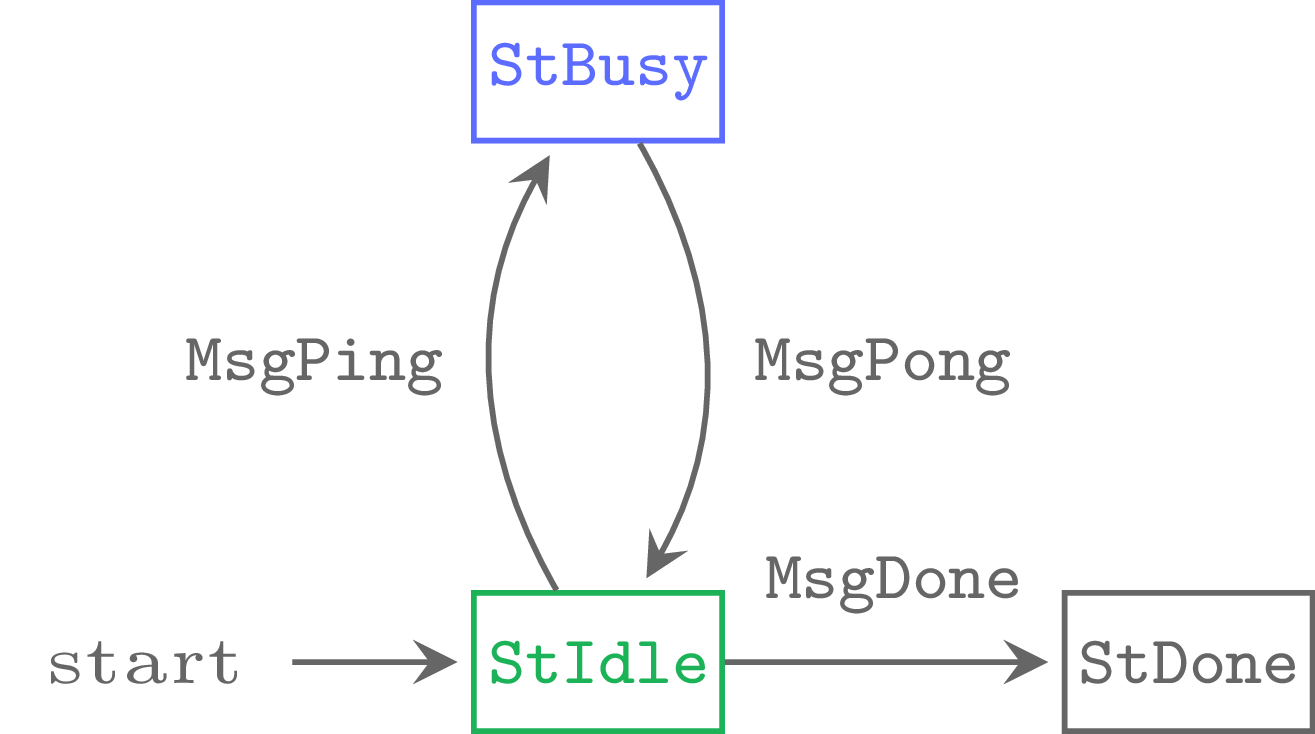
Each arrow designates a message send, the colour of a state signifies its agency, e.g. who is responsible for sending the message. For example MsgPing is send by the client (green), it also shifts agency from client to server: in the StBusy state the server holds agency and thus is responsible for sending messages. Not all messages need to transfer agency, we will consider such an extension to the PingPong protocol later.

The typed-protocols package restricts the way an application executing a protocol can be build and makes it correct by construction. Using type-level programming, one can only construct applications which obey state machine rules faithfully represented by types. A detailed exposition of the package where given at Haskell-eXchange by Duncan Coutts, or my longer workshop at Monadic Party: part 1, part 2, part 3. For example one might construct a client which explores the following state changes:

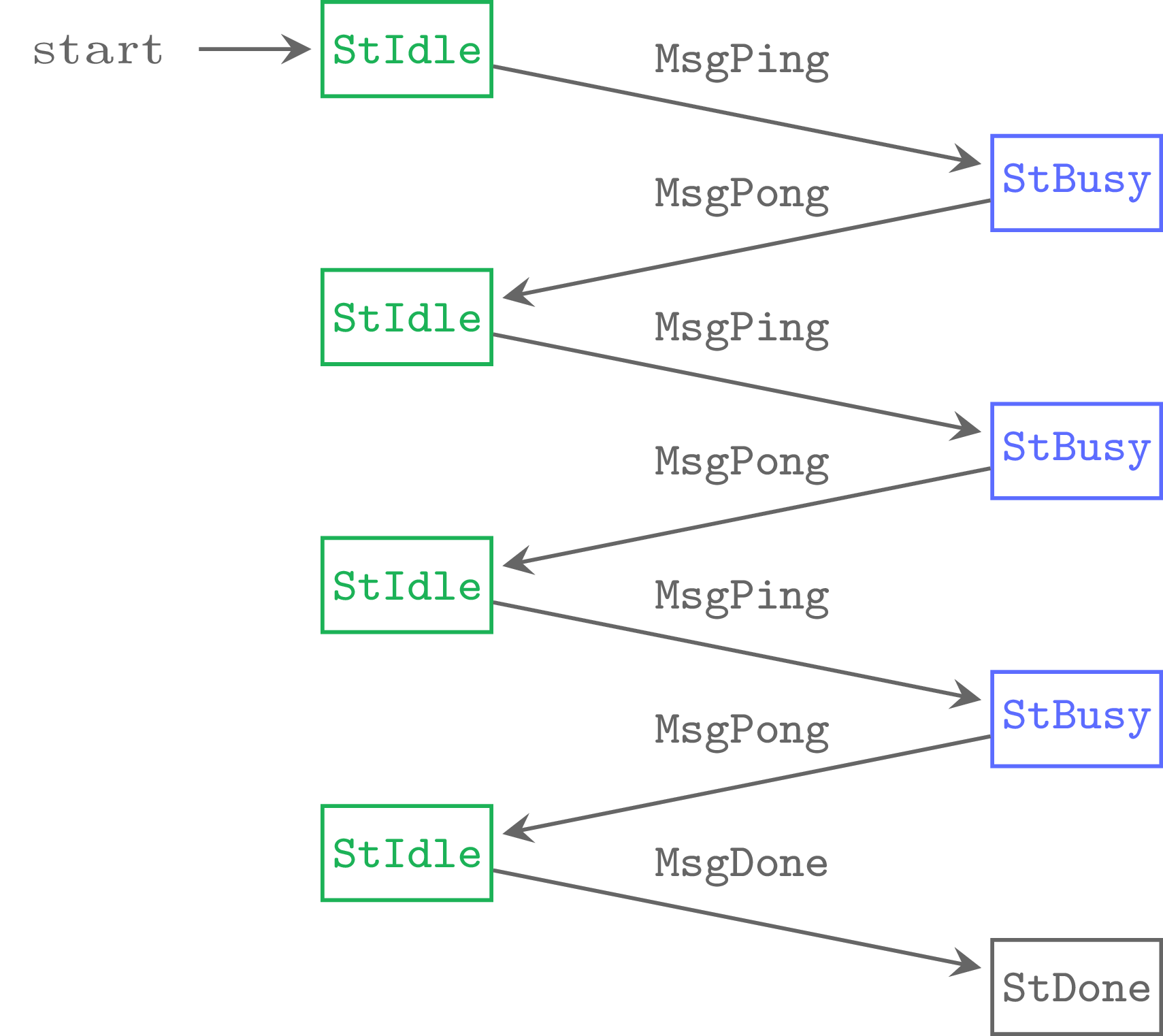
The client will send MsgPing and await for MsgPong before sending next MsgPing. If we’d like to pipeline all the MsgPing the communication would look like:

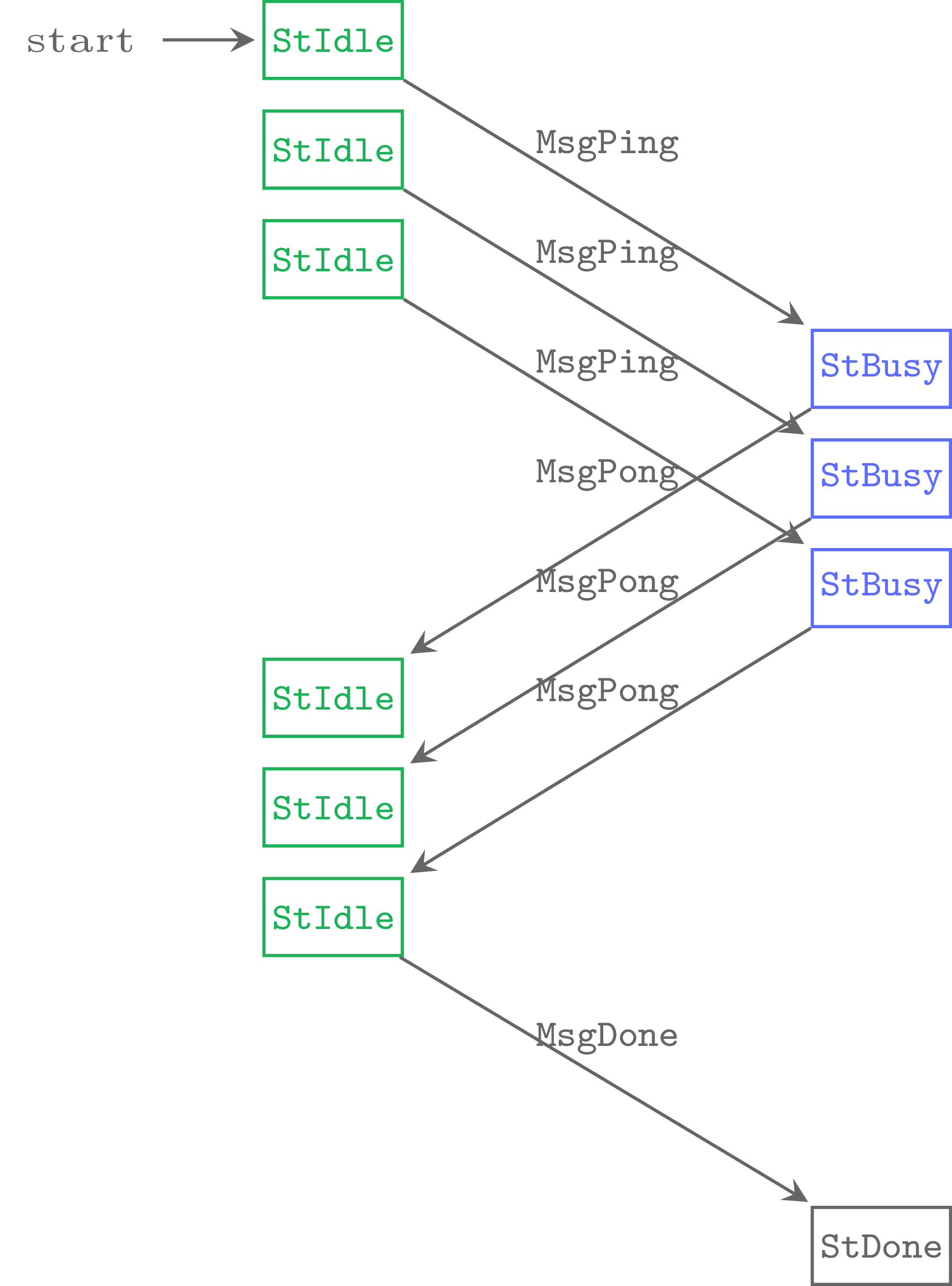
where now we don’t wait for a response before sending next request.

The most important difference between these two diagrams is that the pipelined version is no longer a continuous flow. Pipelining breaks the composition of transitions. Instead, we promise to do some of the transitions at a later time. This delayed processing needs to be managed by the protocol execution environment. What is worth noting that we must keep the order of transitions. In the ping pong protocol this is not readily visible in types as we only collect MsgPong messages, but one could easily imagine a more complex protocol in which it would matter. It is not difficult to envision that queues enter the picture as we need the first-in first-out semantics.

Our current implementation of pipelining in typed-protocols, which in simplified form we will reconstruct for the purpose of this blog post, is using a pair of threads communicating through a pair of queues. The mix of concurrency and type level programming was a neat idea by Duncan Coutts.

In this post we will explore how to re-implement pipelining which does not involve branching and instead use type level programming to give a non-branching recursive api for pipelining, which can be interpreted without the need of concurrency. As we will see, this will improve the way pipelined protocols can be expressed, at the expense of using additional advanced type level programming machinery (since typed-protocols already rely on similar techniques this is not a concern here).

Towards non-pipelined protocol description

This is our first simplest attempt to encode a non-pipelined ping-pong client. The client can be in either of the three states:

data PingPong where
  StIdle :: PingPong
  StBusy :: PingPong
  StDone :: PingPong

It can send either of the messages:

data MessageSimplePingPong (st :: PingPong) (st' :: PingPong) where
  MsgSimplePing :: MessageSimplePingPong StIdle StBusy
  MsgSimplePong :: MessageSimplePingPong StBusy StIdle
  MsgSimpleDone :: MessageSimplePingPong StIdle StDone

Now a client can be encoded as a recursive data type (although this representation is not very useful as it does not allow to do any IO):

data SimplePingPongClient (st :: PingPong) a where
  SendMsg    :: MessageSimplePingPong StIdle st
             -> (SimplePingPongClient st a)
             -> SimplePingPongClient StIdle a

  RecvMsg    :: (MessageSimplePingPong StBusy StIdle
                  -> (SimplePingPongClient StIdle a))
             -> SimplePingPongClient StBusy a

  ClientDone :: a
             -> SimplePingPongClient StDone a

Our initial example client which sends a ping message, awaits for the response, loops it two more times and sends the terminating message can be written as:

simplePingPongClient :: a -> SimplePingPongClient StIdle a
simplePingPongClient a =
    SendMsg MsgSimplePing
  $ RecvMsg $ \MsgSimplePong ->
    SendMsg MsgSimplePing
  $ RecvMsg $ \MsgSimplePong ->
    SendMsg MsgSimplePing
  $ RecvMsg $ \MsgSimplePong ->
    SendMsg MsgSimpleDone
  $ ClientDone a

How to represent pipelining

The SimplePingPongClient does not allow us to write a client which pipelines messages.

The idea is that we can separate the sender side from the receiver. Together with a pipelined message we need to present a receiver and a continuation which can send more messages. On the type level we only need to track the number of outstanding pipelined messages. For this we use an inductive natural numbers:

-- | Type level inductive natural numbers.
--
data N = Z | S N

data SimplePipelinedPingPongClient (st :: PingPong) (n :: N) c a where
  -- | Pipeline a single message, together with a receiver and a continuation
  -- with incremented outstanding message counter.
  --
  PipelinedSendMsg :: MessageSimplePingPong StIdle st
                   -> PingPongReceiver              StBusy StIdle c
                   -> SimplePipelinedPingPongClient StIdle (S n) c a
                   -> SimplePipelinedPingPongClient StIdle    n  c a

  -- | Collect the receiver result.  The continuation subtracts from
  -- outstanding pipelined message counter.
  --
  CollectResponse  :: (c -> SimplePipelinedPingPongClient StIdle n c a)
                   -> SimplePipelinedPingPongClient StIdle (S n) c a

  -- | Send terminal message; it is only allowed once we collected all the
  -- responses.
  --
  SendMsgDone      :: MessageSimplePingPong StIdle StDone
                   -> SimplePipelinedPingPongClient StDone Z c a
                   -> SimplePipelinedPingPongClient StIdle Z c a

  -- | Once terminating message was sent, return.
  --
  PipelinedDone    :: a
                   -> SimplePipelinedPingPongClient StDone Z c a

-- | Receiver; callback which is called on each 'MsgPong' received.
--
data PingPongReceiver (st :: PingPong) (st' :: PingPong) c where
  RecvPipelinedMsg :: (MessageSimplePingPong StBusy StIdle -> c)
                   -> PingPongReceiver StBusy StIdle c

-- | Pipelined ping pong client, which for simplicity pipelines two messages
--
simplePipelinedPingPongClient
   :: a -- ^ fixed result, for simplicity
   -> c -- ^ fixed collected value, for simplicity
   -> SimplePipelinedPingPongClient StIdle Z c a
simplePipelinedPingPongClient a c =
   PipelinedSendMsg
     MsgSimplePing
     (RecvPipelinedMsg $ \MsgSimplePong -> c)
     (PipelinedSendMsg MsgSimplePing
                       (RecvPipelinedMsg $ \MsgSimplePong -> c)
                       (CollectResponse $ \_c0 ->
                          CollectResponse $ \_c1 ->
                            SendMsgDone MsgSimpleDone $
                              PipelinedDone a
                       )
     )

This is a simplified version of pipelining api implemented in typed-protocols. There are a few minor problems with this approach:

the recursive flow of SimplePingPongClient is broken
in complex protocols one needs to share the type c between all the possibly different pipelining scenarios

The SimplePipelinedPingPongClient still needs an interpreter. Let’s try to envision how it could look like. In the network context we can consider that we are given a bidirectional bearer with guaranteed ordered delivery of messages. Let’s envision its interface as:

data PingPongChannel m = PingPongChannel {
    sendMsg :: forall st st'. MessageSimplePingPong st st' -> m (),
    readMsg :: forall st st'. m (MessageSimplePingPong st st')
  }

For the real implementation look here.

The SimplePipeliendPingPongClient interpreter should be a function of this type

runPingPongClient :: PingPongChannel m
                  -> SimplePipelinedPingPongClient st n c a
                  -> m a

The question is how could we deal with PipelinedSendMsg which branches between receiver and a continuation? The solution in typed-protocols is to run two threads and communicate between them with a pair of queues. Once we need to interpret PipelinedSendMsg we would push the receiver to the queue, send a message through the PingPongChannel and continue. There would be another thread that would read that queue and interpret the receiver with:

runPingPongReceiver :: PingPongChannel m
                    -> PingPongReceiver st st' c
                    -> m c

It reads from the network, execute the receiver’s callback and write the result (of type c) to the other queue, from which it would be available to runPingPongClient when interpreting CollectResponse (ref. runPipelinedPeerWithDriver).

Protocol description

So far we tried to present a single client in a type safe way. In general we’d like to be able to represent a wide class of binary protocols, and for each protocol to be able to construct both sides: client and/or server. The following Protocol type class together with auxiliary types PeerRole and PeerHasAgency defines what is needed to construct a protocol and proofs of its correctness. So far we’ve only used Message type from this type class. Each protocol has to define which side has the agency at each state and which states are terminating; for this the type class has to provide ClientHasAgency, ServerHasAgency and NobodyHasAgency together with some lemmas that ensure correctness of the provided associated data instances.

class Protocol ps where

  -- | The messages for this protocol. It is expected to be a GADT that is
  -- indexed by the @from@ and @to@ protocol states. That is the protocol state
  -- the message transitions from, and the protocol state it transitions into.
  -- These are the edges of the protocol state transition system.
  --
  data Message ps (st :: ps) (st' :: ps)

  -- | Tokens for those protocol states in which the client has agency.
  --
  data ClientHasAgency (st :: ps)

  -- | Tokens for those protocol states in which the server has agency.
  --
  data ServerHasAgency (st :: ps)

  -- | Tokens for terminal protocol states in which neither the client nor
  -- server has agency.
  --
  data NobodyHasAgency (st :: ps)

  -- | If the client has agency for a state, there are no
  -- cases in which the server has agency for the same state.
  --
  exclusionLemma_ClientAndServerHaveAgency
    :: forall (st :: ps).
       ClientHasAgency st
    -> ServerHasAgency st
    -> Void

  -- | If nobody has agency for a state (the state is terminating), there
  -- are no cases in which the client has agency for the same state.
  --
  exclusionLemma_NobodyAndClientHaveAgency
    :: forall (st :: ps).
       NobodyHasAgency st
    -> ClientHasAgency st
    -> Void

  -- | If nobody has agency for a state (the state is terminating), there
  -- are no cases in which the server has agency for the same state.
  --
  exclusionLemma_NobodyAndServerHaveAgency
    :: forall (st :: ps).
       NobodyHasAgency st
    -> ServerHasAgency st
    -> Void

data PeerRole = AsClient | AsServer

type PeerHasAgency :: PeerRole -> ps -> Type
data PeerHasAgency    pr          st where
    ClientAgency :: !(ClientHasAgency st) -> PeerHasAgency AsClient st
    ServerAgency :: !(ServerHasAgency st) -> PeerHasAgency AsServer st

type WeHaveAgency   (pr :: PeerRole) st = PeerHasAgency             pr  st
type TheyHaveAgency (pr :: PeerRole) st = PeerHasAgency (FlipAgency pr) st
type family FlipAgency (pr :: PeerRole) where
    FlipAgency AsClient = AsServer
    FlipAgency AsServer = AsClient

We have six exclusive states: client has agency, server has agency or both terminated and three forbidden states by exclusion lemmas: client and server have agency, client has agency and server terminated, client terminated and server has agency.

Pipelining with type level queue

We already seen that pipelining requires a queue that allows to send more messages before waiting for the replies. But it does not necessarily needs to be a term level queue, equally well we could push the expected transitions on a type level queue, and give a way to collect responses and thus eliminate from the type level queue.

`Queue` kind

First let us define elements that will be pushed on to the queue. When we just send some Message pt from to and we want to pipeline next message Message from' to', we will push Tr to from' onto the queue. The Tr to from' :: Trans ps is a promoted type which allows us to track delayed transitions.

data Trans ps where
    Tr :: forall ps. ps -> ps -> Trans ps

We represent the type level queue with type level list. <| and Empty are simply type aliases, we also provide a snoc operator |> which we will use to push elements onto the queue.

-- | Queue kind
--
data Queue ps where
  Empty :: Queue ps
  Cons  :: Trans ps -> Queue ps -> Queue ps

-- | Cons type alias
--
type  (<|) :: Trans ps -> Queue ps -> Queue ps
type a <| as = Cons a as
infixr 5 <|

-- | Snoc operator
--
type (|>) :: Queue ps -> Trans ps -> Queue ps
type family as |> b where
     Empty     |> b = Cons b Empty
     (a <| as) |> b = a <| (as |> b)
infixr 5 |>

`Peer`

The PeerPiplined type is a general API for building protocol applications which satisfy the Protocol type class constraint. Unlike our previous examples it can be used to build either client or server roles. The client and server build with it are necessarily dual to each other, see theorem_duality below. It also supports any monad and can embed any monadic computations.

-- | Promoted data type which indicates if 'Peer' is used in
-- pipelined mode or not.
--
data Pipelined = NonPipelined | Pipelined

type Peer :: forall ps
          -> PeerRole
          -> Pipelined
          -> Queue ps
          -> ps
          -> (Type -> Type)
          -> Type
          -> Type
data Peer ps pr pl q st m a where

    -- | 'Effect' allows to introduce monadic effects.
    --
    Effect
      :: m (Peer ps pr pl q st m a)
      ->    Peer ps pr pl q st m a

    -- | Non-pipelined send.  One needs to present proof of agency, message
    -- to be send and a continuation.  One cannot send
    -- non-pipelined messages when there are outstanding requests.  This is
    -- enforced by requiring that the queue is empty.
    --
    Yield
      :: !(WeHaveAgency pr st)
      -> Message ps st st'
      -> Peer ps pr pl Empty st' m a
      -> Peer ps pr pl Empty st  m a

    -- | Await for a non-pipelined message.  One has to present a proof that
    -- one does not have agency and a continuation function which can deal
    -- with any message that might arrive from the network.
    --
    Await
      :: !(TheyHaveAgency pr st)
      -> (forall st'. Message ps st st'
          -> Peer ps pr pl Empty st' m a)
      -> Peer     ps pr pl Empty st  m a

    -- | Terminate the protocol.
    --
    Done
      :: !(NobodyHasAgency st)
      -> a
      -> Peer ps pr pl Empty st m a

    --
    -- Pipelining primitives
    --

    -- | Pipelined send which. Note that the continuation decides from which
    -- state we pipeline next message, and the gap is pushed at the back of
    -- the queue.
    --
    YieldPipelined
      :: !(WeHaveAgency pr st)
      -> Message ps st st'
      -> Peer ps pr 'Pipelined (q |> Tr st' st'') st'' m a
      -> Peer ps pr 'Pipelined  q                 st   m a

    -- | Partially collect promised transition.
    --
    Collect
      :: Maybe (Peer ps pr 'Pipelined (Tr st' st'' <| q) st m a)
      -> !(TheyHaveAgency pr st')
      -> (forall stNext. Message ps st' stNext
          -> Peer ps pr 'Pipelined (Tr stNext st'' <| q) st m a)
      -> Peer     ps pr 'Pipelined (Tr st'    st'' <| q) st m a

    -- | Collect the identity transition.
    --
    -- 'CollectDone' allows to defer popping @Tr ps st st@ from the queue
    -- after a message is received (in 'Collect' callback), unlike 'Collect'
    -- which needs to know the transition type at compile time.
    --
    CollectDone
      :: Peer ps pr 'Pipelined              q  st m a
      -> Peer ps pr 'Pipelined (Tr st st <| q) st m a

`PingPong` protocol

In this section we will formalise the ping pong protocol by providing Protocol instance.

instance Protocol PingPong where
  -- | Ping pong messages
  --
  data Message PingPong from to where
    MsgPing :: Message PingPong StIdle StBusy
    MsgPong :: Message PingPong StBusy StIdle
    MsgDone :: Message PingPong StIdle StDone

  data ClientHasAgency st where
    TokIdle :: ClientHasAgency StIdle

  data ServerHasAgency st where
    TokBusy :: ServerHasAgency StBusy

  data NobodyHasAgency st where
    TokDone :: NobodyHasAgency StDone

  -- exclusion lemmas, which prove that n each state at most one of server, or
  -- client has agency.
  exclusionLemma_ClientAndServerHaveAgency TokIdle tok = case tok of {}
  exclusionLemma_NobodyAndClientHaveAgency TokDone tok = case tok of {}
  exclusionLemma_NobodyAndServerHaveAgency TokDone tok = case tok of {}

Some auxiliary instances:

deriving instance Show (Message PingPong from to)
deriving instance Show (ClientHasAgency (st :: PingPong))
deriving instance Show (ServerHasAgency (st :: PingPong))

Non-pipelined ping pong client

-- A non-pipelined PingPong.
--
pingPongClient
   :: a -> Peer PingPong AsClient NonPipelined Empty StIdle m a
pingPongClient a =
     -- send ping message
     Yield (ClientAgency TokIdle) MsgPing
     -- await for the response
   $ await
   $ Yield (ClientAgency TokIdle) MsgPing
   $ await
   $ -- send terminating message
     Yield (ClientAgency TokIdle) MsgDone
     -- return
   $ Done TokDone a
 where
  -- await for all 'MsgPong' until first 'MsgPongDone'
  await :: Peer PingPong AsClient NonPipelined Empty StIdle m a
        -> Peer PingPong AsClient NonPipelined Empty StBusy m a
  await k =
    Await (ServerAgency TokBusy) $ \msg ->
      case msg of
        MsgPong -> k

Pipelined ping pong client

-- A pipelined 'PingPong', without partial collects.
--
pingPongClientPipelined
   :: a -> Peer PingPong AsClient 'Pipelined Empty StIdle m a
pingPongClientPipelined a =
     -- pipeline three pings
     YieldPipelined (ClientAgency TokIdle) MsgPing
   $ YieldPipelined (ClientAgency TokIdle) MsgPing
   $ YieldPipelined (ClientAgency TokIdle) MsgPing
     -- collect three pongs
   $ collect
   $ collect
   $ collect
   $ Yield (ClientAgency TokIdle) MsgDone
     -- return from the protocol
   $ Done TokDone a
 where
   collect :: Peer PingPong AsClient 'Pipelined q  StIdle m a
           -> Peer PingPong AsClient 'Pipelined
                           (Tr StBusy StIdle <| q) StIdle m a
   collect k =
       Collect Nothing (ServerAgency TokBusy)
     $ \msg -> case msg of
         MsgPong -> CollectDone k

`PingPong2` protocol

Let us consider a variation of the ping pong protocol, in which the server might send multiple MsgBusy before transferring agency back to the client with MsgPong. In this version by pipelining MsgPing, we might need to collect multiple MsgBusy until we receive MsgPong. It will help us demonstrate that we can pipeline multiple MsgPing messages and collect all the replies.

-- | PingPong2 has the same state machine, although we will a different
-- `Protocol` instance.  For that reason we provide a newtype wrapper and
-- use type aliases.
--
newtype PingPong2 = Wrap PingPong
type StIdle2 = Wrap StIdle
type StBusy2 = Wrap StBusy
type StDone2 = Wrap StDone

instance Protocol PingPong2 where
  data Message PingPong2 from to where
    -- | 'PingPong' message
    MsgPingPong  :: Message PingPong        st            st'
                 -> Message PingPong2 (Wrap st)     (Wrap st')
    -- | new message
    MsgBusy      :: Message PingPong2 (Wrap StBusy) (Wrap StBusy)

  data ClientHasAgency st where
    WrapClient :: ClientHasAgency       st
               -> ClientHasAgency (Wrap st)

  data ServerHasAgency st where
    WrapServer :: ServerHasAgency       st
               -> ServerHasAgency (Wrap st)

  data NobodyHasAgency st where
    WrapDone   :: NobodyHasAgency       st
               -> NobodyHasAgency (Wrap st)

  -- We haven't changed the states and their agencies, so we can reuse
  -- 'PingPong' lemmas.
  exclusionLemma_ClientAndServerHaveAgency (WrapClient tok) (WrapServer tok') =
    exclusionLemma_ClientAndServerHaveAgency tok tok'
  exclusionLemma_NobodyAndClientHaveAgency (WrapDone   tok) (WrapClient tok') =
    exclusionLemma_NobodyAndClientHaveAgency tok tok'
  exclusionLemma_NobodyAndServerHaveAgency (WrapDone   tok) (WrapServer tok') =
    exclusionLemma_NobodyAndServerHaveAgency tok tok'

Some auxiliary instances:

deriving instance Show (Message PingPong2 from to)
deriving instance Show (ClientHasAgency (st :: PingPong2))
deriving instance Show (ServerHasAgency (st :: PingPong2))

Pipelined ping pong client using `Collect`

-- | A pipelined 'PingPong' which supports partial collects using the
-- recursive 'collect'.
--
pingPongClientPipelined2
  :: a
  -> Peer PingPong2 AsClient 'Pipelined Empty StIdle2 m a
pingPongClientPipelined2 a =
      -- pipeline three 'MsgPing'
      YieldPipelined (ClientAgency (WrapClient TokIdle)) (MsgPingPong MsgPing)
    $ YieldPipelined (ClientAgency (WrapClient TokIdle)) (MsgPingPong MsgPing)
    $ YieldPipelined (ClientAgency (WrapClient TokIdle)) (MsgPingPong MsgPing)
      -- collect responses
    $ collect
    $ collect
    $ collect
    $ Yield (ClientAgency (WrapClient TokIdle)) (MsgPingPong MsgDone)
    $ Done (WrapDone TokDone) a
  where
    -- recursively collect responses, until 'MsgPongDone2' is received
    collect :: Peer PingPong2 AsClient 'Pipelined q  StIdle2 m a
            -- ^ continuation after removing @Tr StBusy2 StIdle2@ from the
            -- queue
            -> Peer PingPong2 AsClient 'Pipelined
                           (Tr StBusy2 StIdle2 <| q) StIdle2 m a
    collect k =
        Collect Nothing (ServerAgency (WrapServer TokBusy))
      $ \msg -> case msg of
          MsgBusy               -> collect     k
          (MsgPingPong MsgPong) -> CollectDone k

Next example is similar to the previous one but it counts the number of MsgBusy received.

pingPongClientPipelined2Counter
    :: Peer PingPong2 AsClient 'Pipelined Empty StIdle2 m Int
pingPongClientPipelined2Counter =
      -- pipeline three 'MsgPing2'
      YieldPipelined (ClientAgency (WrapClient TokIdle)) (MsgPingPong MsgPing)
    $ YieldPipelined (ClientAgency (WrapClient TokIdle)) (MsgPingPong MsgPing)
    $ YieldPipelined (ClientAgency (WrapClient TokIdle)) (MsgPingPong MsgPing)
      -- collect responses, and count received 'MsgBusy'
    $        collect 0
    $ \n1 -> collect n1
    $ \n2 -> collect n2
    $ \n3 -> Yield (ClientAgency (WrapClient TokIdle)) (MsgPingPong MsgDone)
    $        Done (WrapDone TokDone) n3
  where
    -- recursively collect responses, until 'MsgPongDone2' is received
    collect
        :: Int
        -- ^ number of 'MsgBusy' received so far
        -> (Int -> Peer PingPong2 AsClient 'Pipelined q  StIdle2 m Int)
        -- ^ continuation after removing @Tr StBusy2 StIdle2@ from the
        -- queue
        -> Peer PingPong2 AsClient 'Pipelined
                               (Tr StBusy2 StIdle2 <| q) StIdle2 m Int
    collect !n k =
        Collect Nothing (ServerAgency (WrapServer TokBusy))
      $ \msg -> case msg of
          MsgBusy               -> collect     (n+1) k
          (MsgPingPong MsgPong) -> CollectDone      (k n)

Duality

Duality assures that two peers in dual roles: AsClient vs AsServer can run a protocol without deadlock. We also prove that if a protocol will terminate both sides will end at a common terminal state (one of the states in which NobodyHasAgency). The proofs holds under the assumption that the encoding of messages is 1-1, if this assumption is not true it is possible that an application will not terminate when reaching a terminal state, or that it will terminate early causing the other side to deadlock. There are situations when non injective codecs are useful, and these cases require additional care.

Duality for non-pipelined protocols

First we start with duality for non-pipelined protocols, as this is quite a bit simpler. The code below is copy-paste from typed-protocols package (with small adjustments).

data TerminalStates ps where
  TerminalStates :: forall ps (st :: ps) (st' :: ps).
                    NobodyHasAgency st
                 -> NobodyHasAgency st'
                 -> TerminalStates ps

theorem_nonpipelined_duality
   :: forall ps (pr :: PeerRole) (initSt :: ps) m a b.
      ( Monad m, Protocol ps)
   => Peer ps             pr  NonPipelined Empty initSt m a
   -> Peer ps (FlipAgency pr) NonPipelined Empty initSt m b
   -> m (a, b, TerminalStates ps)
theorem_nonpipelined_duality = go
  where
    go :: forall (st :: ps).
          Peer ps             pr  NonPipelined Empty st m a
       -> Peer ps (FlipAgency pr) NonPipelined Empty st m b
       -> m (a, b, TerminalStates ps)
    go (Done stA a)    (Done stB b)    = return (a, b, TerminalStates stA stB)
    go (Effect a )      b              = a >>= \a' -> go a' b
    go  a              (Effect b)      = b >>= \b' -> go a  b'
    go (Yield _ msg a) (Await _ b)     = go  a     (b msg)
    go (Await _ a)     (Yield _ msg b) = go (a msg) b

    -- By appealing to the proofs about agency for this protocol we can
    -- show that these other cases are impossible
    go (Yield (ClientAgency stA) _ _) (Yield (ServerAgency stB) _ _) =
      absurd (exclusionLemma_ClientAndServerHaveAgency stA stB)

    go (Yield (ServerAgency stA) _ _) (Yield (ClientAgency stB) _ _) =
      absurd (exclusionLemma_ClientAndServerHaveAgency stB stA)

    go (Await (ClientAgency stA) _)   (Await (ServerAgency stB) _)   =
      absurd (exclusionLemma_ClientAndServerHaveAgency stA stB)

    go (Await (ServerAgency stA) _)   (Await (ClientAgency stB) _)   =
      absurd (exclusionLemma_ClientAndServerHaveAgency stB stA)

    go (Done  stA _)            (Yield (ServerAgency stB) _ _) =
      absurd (exclusionLemma_NobodyAndServerHaveAgency stA stB)

    go (Done  stA _)            (Yield (ClientAgency stB) _ _) =
      absurd (exclusionLemma_NobodyAndClientHaveAgency stA stB)

    go (Done  stA _)            (Await (ServerAgency stB) _)   =
      absurd (exclusionLemma_NobodyAndServerHaveAgency stA stB)

    go (Done  stA _)            (Await (ClientAgency stB) _)   =
      absurd (exclusionLemma_NobodyAndClientHaveAgency stA stB)

    go (Yield (ClientAgency stA) _ _) (Done stB _)    =
      absurd (exclusionLemma_NobodyAndClientHaveAgency stB stA)

    go (Yield (ServerAgency stA) _ _) (Done stB _)    =
      absurd (exclusionLemma_NobodyAndServerHaveAgency stB stA)

    go (Await (ClientAgency stA) _)   (Done stB _)    =
      absurd (exclusionLemma_NobodyAndClientHaveAgency stB stA)

    go (Await (ServerAgency stA) _)   (Done stB _)    =
      absurd (exclusionLemma_NobodyAndServerHaveAgency stB stA)

Removing pipelining

We can show that any peer that is using pipelining primitives can be transformed into non-pipelined version. This is possible because pipelining does not changes the order of messages sent or received. We just need to track this order with PrQueue. First we define various singletons needed to track the evolution of types.

-- | Singletons for types of kind `Trans`.
--
type STrans :: Trans ps -> Type
data STrans tr where
   STr :: STrans (Tr st st')

-- | Singleton for types of kind `Queue` kind.
---
type SQueue :: Queue ps -> Type
data SQueue q where
  SEmpty :: SQueue Empty
  SCons  :: STrans (Tr st st') -> SQueue q -> SQueue (Tr st st' <| q)

-- | `PrQueue` tracks the order of transitions.  We either have an
-- explicit `Message` or a `STrans` singleton, both are pushed by
-- `YieldPipelined` operation.
--
-- Note: if not the order of arguments 'PrQueue' could be given a category
-- instance
type PrQueue :: forall ps -> PeerRole -> ps -> Queue ps -> ps -> Type
data PrQueue ps pr st q st' where
  ConsMsgQ :: WeHaveAgency pr st
           -> Message ps st st'
           -> PrQueue ps pr st' q st''
           -> PrQueue ps pr st  q st''

  ConsTrQ  :: STrans (Tr st st')
           -> PrQueue ps pr st'               q  st''
           -> PrQueue ps pr st  (Tr st st' <| q) st''

  EmptyQ   :: PrQueue ps pr st Empty st

-- | Push a `ConsMsgQ` to the back of `PrQueue`.
--
snocMsgQ :: WeHaveAgency pr st'
         -> Message ps st' st''
         -> PrQueue ps pr st q st'
         -> PrQueue ps pr st q st''
snocMsgQ stok msg (ConsMsgQ stok' msg' pq) =
  ConsMsgQ stok' msg' (snocMsgQ stok msg pq)
snocMsgQ stok msg (ConsTrQ str pq) =
  ConsTrQ str (snocMsgQ stok msg pq)
snocMsgQ stok msg EmptyQ =
  ConsMsgQ stok msg EmptyQ

-- | Push a `STrans (Tr st st')` to the back of `PrQueue`.
--
snocTrQ :: STrans (Tr st' st'')
        -> PrQueue ps pr st  q                 st'
        -> PrQueue ps pr st (q |> Tr st' st'') st''
snocTrQ tr (ConsMsgQ stok msg pq) =
  ConsMsgQ stok msg (snocTrQ tr pq)
snocTrQ tr (ConsTrQ tr' pq) =
  ConsTrQ tr' (snocTrQ tr pq)
snocTrQ tr EmptyQ =
  ConsTrQ tr EmptyQ

With all the singletons at hand we are ready to prove:

theorem_unpipeline
    :: forall ps (pr :: PeerRole) (pl :: Pipelined) (initSt :: ps) m a.
       Functor m
    => [Bool]
    -- ^ interleaving choices for pipelining allowed by
    -- `Collect` primitive. False values or `[]` give no
    -- pipelining.
    -> Peer ps (pr :: PeerRole) pl           Empty initSt m a
    -> Peer ps  pr              NonPipelined Empty initSt m a
theorem_unpipeline cs0 = go cs0 EmptyQ
  where
    go :: [Bool]
       -> PrQueue       ps pr            st q     st'
       -> Peer ps pr pl            q     st' m a
       -> Peer ps pr 'NonPipelined Empty st  m a

    go cs pq     (Effect k)         = Effect         $ go cs pq <$> k
    go cs EmptyQ (Yield stok msg k) = Yield stok msg $ go cs EmptyQ k
    go cs EmptyQ (Await stok k)     = Await stok     $ go cs EmptyQ . k
    go _  EmptyQ (Done stok a)      = Done  stok a

    go cs pq     (YieldPipelined stok msg k) =
       -- push message and promised transition to `PrQueue`.
       go cs ( pq
             & snocMsgQ stok msg
             & snocTrQ STr
             )
             k

    go cs (ConsMsgQ stok msg pq) k  = Yield stok msg $ go cs pq k

    go (True:cs')    pq  (Collect (Just k) _ _) =
       go cs' pq k
    go cs (ConsTrQ _ pq) (Collect _ stok k) =
       Await stok $ go cs (ConsTrQ STr pq) . k

    go cs (ConsTrQ _ pq) (CollectDone k) =
       go cs pq k

Duality for pipelined protocols

The proof of our main theorem is a straight forward consequence of our earlier results:

theorem_duality
    :: forall ps (pr :: PeerRole) (pl :: Pipelined) (st :: ps) m a b.
       ( Monad m, Protocol ps )
    => [Bool]
    -> [Bool]
    -> Peer ps             pr  pl Empty st m a
    -> Peer ps (FlipAgency pr) pl Empty st m b
    -> m (a, b, TerminalStates ps)
theorem_duality csA csB a b =
    theorem_nonpipelined_duality (theorem_unpipeline csA a)
                                 (theorem_unpipeline csB b)

Alternative Agda implementation

There is available an alternative implementation of typed-protocols in Agda, see here. The Agda implementation has a nicer interface. The Haskell implementation needs to provide Protocol instance, which requires to define:

message type
agency singletons for each state
a set of three proofs that verify that a state singleton is provided for only one agency type: either ClientHasAgency, ServerHasAgency, NobodyHasAgency.

The Agda implementation however makes an explicit distinction between objective agency (ClientAgency, ServerAgency, NobodyAgency) and a relative agency (WeHaveAgency, TheyHaveAgency, NobodyHasAgency), and is indexed over:

message type
a (type level) function from states to the objective agency

The exclusion lemmas are proven for all protocols which are provided with this interface. One still needs to provide agency witnesses for Peer primitives, but they one only can provide them with propositional equality _≡_ (which is equivalent to Haskell’s :~:), and hence simpler to use.

The simplification found in Agda implementation is a future possible improvement in typed-protocols.