Kleisli Categories and Free Monads

Given a monad m one can construct the Kleisli category Control.Arrow.Kleisli m, in this post we’ll explore what happens when we start with a free monad.

{-# LANGUAGE KindSignatures      #-}
{-# LANGUAGE ScopedTypeVariables #-}
{-# LANGUAGE RankNTypes          #-}
module KleisliCategoriesAndFreeMonads where

import Prelude hiding (id, (.))
import Control.Category (Category (id, (.)))
import Control.Monad (ap, join)
import Data.Kind (Type)

Kleisli construction

newtype Kleisli m a b = Kleisli { runKleisli :: a -> m b }

instance Monad m => Category (Kleisli m) where
  id = Kleisli return
  Kleisli f . Kleisli g = Kleisli (\x -> f =<< g x)

The Kleisli composition is so useful, it has it’s own operator defined in Control.Monad:

(<=<) :: Monad m => (y -> m z) -> (x -> m y) -> x -> m z
f <=< g = \x -> f =<< g x

Free monads

Free monad construction gives you a monad out of a functor. It will satisfy all the monad laws: associativity, and unitality axioms, and it is a universal construction.

data Free f a
  = Return a
  | Free (f (Free f a))

instance Functor f => Functor (Free f) where
  fmap f (Return a) = Return (f a)
  fmap f (Free ff)  = Free (fmap f <$> ff)

instance Functor f => Applicative (Free f) where
  pure = return
  (<*>) = ap

instance Functor f => Monad (Free f) where
  return = Return
  Return a >>= f = f a
  Free ff  >>= f = Free (fmap (>>= f) ff)

The universal property of a free monad can be expressed with a class, which I borrowed from free-algebras package (I don’t include all details that are not important for this blog post; The details where described in this post):

class FreeAlgebra1 (m :: (Type -> Type) -> Type -> Type) where
  -- | Natural transformation that embeds generators into `m`.
  liftFree :: Functor f => f a -> m f a

  -- | The freeness property.
  foldNatFree
    :: forall d f a .
       ( Monad d
       , Functor f
       )
    => (forall x. f x -> d x)
    -- ^ a natural transformation which embeds generators of `m` into `d`
    -> (m f a -> d a)
    -- ^ a morphism from `m f` to `d`

In this blog post whenever we will refer to liftFree and foldNatFree we will actually refer to this instance:

instance FreeAlgebra1 Free where
  liftFree fa = Free (Return <$> fa)
  foldNatFree _nat (Return a) = return a
  foldNatFree nat  (Free ff)  =
    join $ nat $
      (foldNatFree nat) <$> ff -- induction step

You probably recognise Free.liftF and Free.foldFree from the free package.

Instances of this class have the property that to construct a natural transformation from FreeAlgebra1 m => m f to a monad Monad d => d is enough to come up with a natural transformation of functors forall x. f a -> d a. If you’d like to explore more why this class is the right one to speak about freeness, checkout one of my previous posts. Note that the instance for Free follows the structure, and there is no room how to implement the methods: that’s a very common feeling in category theory, which means one is on the right path.

This particular instance satisfies rather interesting laws:

liftFree natural transformation

or as an equation:

fmap g . liftFree == liftFree . fmap g

This is more or less straightforward, just take a look at the definition of liftFree.

foldNatFree natural transformation

or as an equation:

fmap g . foldNatFree nat == foldNatFree nat . fmap g

This one is slightly more involved, and lets prove it:

(foldNatFree nat . fmap g) (Return a)
  = foldNatFree nat (Return (g a))
  = return (g a)
  = fmap g (return a)
  = fmap g (foldNatFree nat (Return a))
  = (fmap g . foldNatFree nat) (Return a)

and

(foldNatFree nat . fmap g) (Free ff)
  = foldNatFree nat (fmap g (Free ff))
  = foldNatFree nat (Free (fmap (fmap g) ff))
  = join $ nat $ foldNatFree nat <$> (fmap (fmap g) ff)
  = join $ nat $ foldNatFree nat <$> fmap g <$> ff
  = join $ nat $ (foldNatFree nat . fmap g) <$> ff
  -- by induction hypothesis
  = join $ nat $ (fmap g . foldNatFree nat) <$> ff
  = join $ nat $ fmap g <$> (foldNatFree nat <$> ff)
  = join $ nat $ fmap (fmap g) (foldNatFree nat <$> ff)
  -- since nat is a natural transformation
  = join $ fmap (fmap g) $ nat (foldNatFree nat <$> ff)
  -- join is a natural transformation
  -- join :: Monad m => m (m a) -> m a
  = fmap g $ join $ $ nat (foldNatFree nat <$<> ff)
  = fmap g $ foldNatFree nat (Free ff)
  = (fmpg g . foldNatFree nat) (Free ff)

Since in our case Free is a functor from the category of (endo-)functors into the category of monads. foldNatFree nat has to ba monad morphism for any nat. This means that the following diagrams commute (or equations hold):

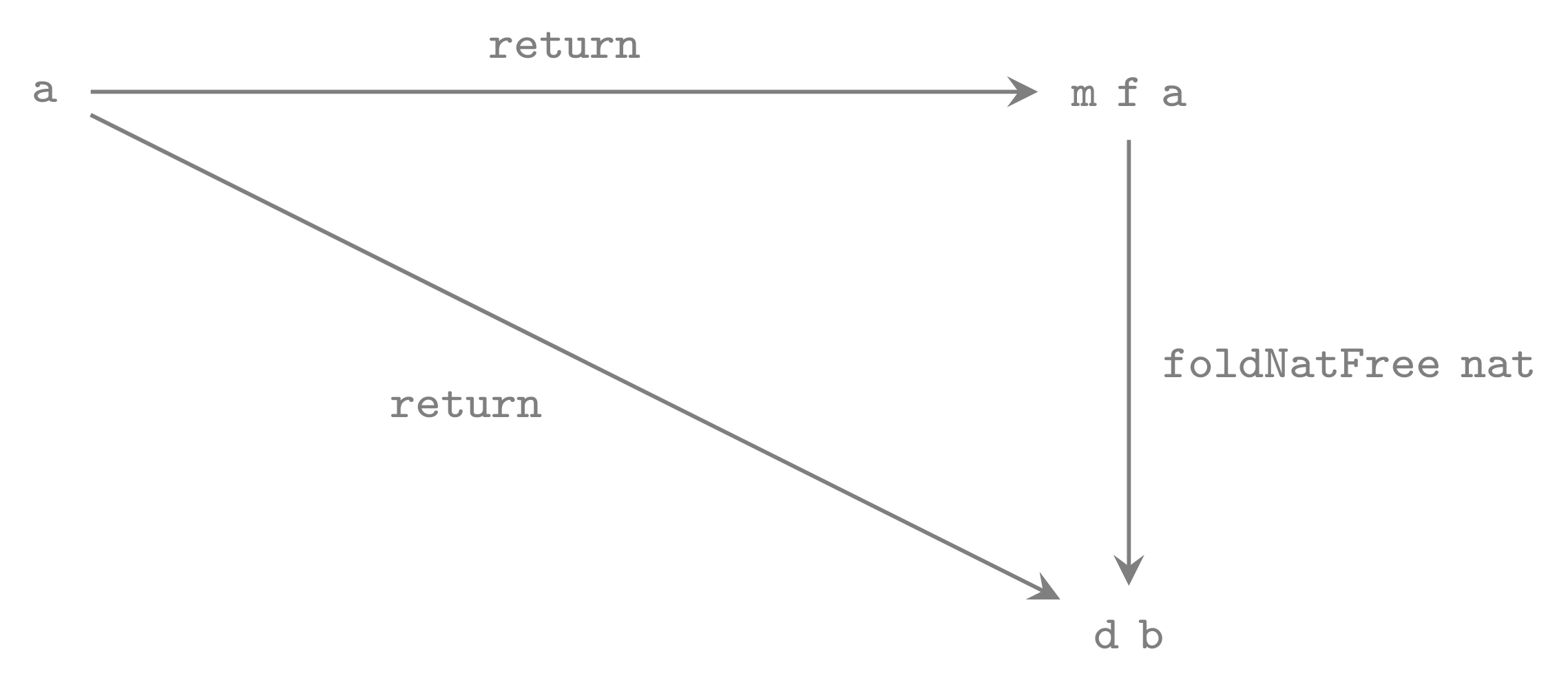
foldNatFree - monad morphism: the unit law

or as an equation:

return = return . foldNatFree nat

This should be clear from definition of foldNatFree. Moreover, the following diagram commutes:

foldNatFree - monad morphism: the join law

or as an equation:

join . (foldNatFree nat . fmap (foldNatFree nat))
  == foldNatFree nat . join

Let us prove this it:

join . (foldNatFree nat . fmap (foldNatFree nat)) (Return (Return a))
  == join (foldNatFree nat (Return (foldNatFree nat (Return a))))
  == join (foldNatFree nat (Return (return a))
  == join (return (return a))
  == return a
  == foldNatFree nat (Return a)
  == foldNatFree nat (join (Return (Return a)))

And the other one, which we prove starting from the right hand side:

foldNatFree nat (join (Free ff)))
  -- by definition of join
  = foldNatFree nat (Free (fmap join ff))
  -- by definition of foldNatFree
  = join $ nat $ fmap (foldNatFree nat) (fmap join ff)
  = join $ nat $ fmap (foldNatFree nat . join) ff
  -- by induction hypothesis
  = join $ nat $ fmap (join . foldNatFree nat . fmap (foldNatFree nat)) ff
  = join $ nat $ fmap join $ fmap (foldNatFree nat) $
      fmap (fmap foldNatFree nat)) ff
  -- since nat is a natural transformation
  = join $ fmap join $ nat $ fmap (foldNatFree nat) $
      fmap (fmap (foldNatFree nat)) ff
  -- by associativity of join
  = join $ join $ nat $ fmap (foldNatFree nat) $
      fmap (fmap (foldNatFree nat)) ff
  -- by definition of foldNatFree (the outer one)
  = join $ foldNatFree nat $ Free $ fmap (fmap (foldNatFree nat)) ff
  -- by definition of functor instance for Free
  = join $ foldNatFree nat $ fmap (foldNatFree nat) $ Free ff
  = (join . foldNatFree nat . fmap (foldNatFree nat)) $ Free ff

Note that by the natural transformation law for foldNatFree we have:

foldNatFree nat . fmap (foldNatFree nat)
  == fmap (foldNatFree nat) . foldNatFree nat

For any monad morphism fn :: (Monad m, Monad n) => m a -> n a, we will show that:

fn . (f <=< g) == (fn . f) <=< (fn . g)

in particular this is true for foldNatFree nat.

(fn . f <=< fn . g)
  == \a -> fn . f =<< (fn . g) a
  == \a -> fn . f =<< fn (g a)
  -- by definition of join (or =<< in terms of a join)
  == \a -> join (fn . f <$> fn (g a))
  -- by functor associativity law
  == \a -> join (fn <$> (f <$> fn (g a)))
  -- since fn is a morphism of monads it is a natural transformation
  -- and thus it commutes with fmap/<$>
  == \a -> join (fn <$> (fn (f <$> g a)))
  -- since fn is a morphism of monads: join (fmap fn . fn) == fn . join
  == \a -> fn (join (f <$> g a))
  -- by definition of join
  == \a -> fn (f =<< g a)
  == \a -> fn (f <=< g) a
  == fn (f <=< g)

The proof could be much shorter if we use monad morphism law in terms of binds. The equivalence form of join (fmap fn . fn) == fn . join expressed with bind is fn (f =<< ma) = (fn . f) =<< fn ma. A reason to use join is that the law take the same form as for monoid homomorphisms, so it is very easy to remember them.

Kleisli categories for free monads

liftKleisli
  :: Monad m
  => Kleisli m a b
  -> Kleisli (Free m) a b
liftKleisli (Kleisli f) = Kleisli (liftFree . f)
foldKleisli
  :: ( Functor f
     , Monad m
     )
  => (forall x. f x -> m x)
  -> Kleisli (Free f) a b
  -> Kleisli m a b
foldKleisli nat (Kleisli f) = Kleisli $ foldNatFree nat . f

This means that Kleisli (Free f) is a free category for the class of graphs of type

Functor f => Kleisli f

(Kleisli f is a category only when f is a monad). Both morphisms: liftKleisli is merely a morphisms of graphs, while foldKleisli is a functor, which means it preserves id and the composition (.) :: Category c => c y z -> c x y -> c x y.

foldKleisli nat id
  == foldKleisli nat (Kleisli Return)
  == Kleisli (foldNatFree nat . Return)
  == Kleisli return
  == id
foldKleisli nat (Kleisli f . Kleisli g)
  == foldKleisli nat (Kleisli f <=< g)
  == Kleisli (foldNatFree nat (f <=< g))
  -- foldNatFree nat is a morphism of monads thus
  == Kleisli (foldNatFree nat f <=< foldNatFree nat g)
  == Kleisli (foldNatFree nat f) . Kleisli (foldNatFree nat g)
  == foldKleisli nat f . foldKleisli nat g