Monadicity

From Algebras to Monads and back to Algebras

In this post I'd like to introduce you to how mathematicians think about monads, and how they are useful. We will study a general case alongside with a simple example of the category of monoids. I hope you will get from this post how a monad describes category of monoids. We will need some simple category theory tools like: adjoint functors, f-algebras, free algebras (or just free monoids) and monads. This blog post is based on a library I recently wrote, and it will use snippets of code from it.

Let Hask be the category of Haskell types and Monoid be the category of monoids in Hask. There are two functors that connect this two categories: $$U:\mathrm{Monoid}\rightarrow\mathrm{Hask}$$ which sends a monoid $m$ to its underlying type forgetting the $Monad$ constraint; and the free monoid functor: $$F:\mathrm{Hask}\rightarrow\mathrm{Monoid}$$ which takes a type $a$ and sends it to the list monoid: $[a]$. Let's try to analyse the relationship between the two functors. If you read my previous post on free algebras it won't be a surprise to you that there is a close relationship between these two constructions.

-- |
-- Type family which for each free algebra @m@ returns a type level
-- lambda from types to constraints.  It is describe the class of
-- algebras for which this free algebra is free. 
type family AlgebraType  (f :: k) (a :: l) :: Constraint

-- |
-- Type family which limits Hask to its full subcategory which
-- satisfies a given constraints.  Some free algebras, like free
-- groups, or free abelian semigroups have additional constraints on
-- on generators, like @Eq@ or @Ord@.
type family AlgebraType0 (f :: k) (a :: l) :: Constraint

-- |
-- A proof that constraint @c@ holds for type @a@.
newtype Proof (c :: Constraint) (a :: l) = Proof (Dict c)

-- |
-- A lawful instance has to guarantee that @'unFoldFree'@ is an inverse
-- of @'foldMapFree'@.
-- 
-- This in turn guaranties that @m@ is a left adjoint functor from Hask
-- to algebras of type @'AlgebraType m'@.  The right adjoint is the
-- forgetful functor.  The composition of left adjoin and the right one
-- is always a monad, this is why we will be able to build monad
-- instance for @m@.
class FreeAlgebra (m :: Type -> Type)  where
    -- | Injective map that embeds generators @a@ into @m@.
    returnFree :: a -> m a
    -- | The freeness property.
    foldMapFree
	:: forall d a
	 . ( AlgebraType m d
	   , AlgebraType0 m a
	   )
	=> (a -> d)   -- ^ map generators of @m@ into @d@
	-> (m a -> d) -- ^ returns a homomorphism from @m a@ to @d@

    -- |
    -- Proof that @AlgebraType0 m a => m a@ is an algebra of type
    -- @AlgebraType m@.  This proves that @m@ is a mapping from the full
    -- subcategory of @Hask@ of types satisfying @AlgebraType0 m a@
    -- constraint to the full subcategory satisfying @AlgebraType m a@,
    -- @fmapFree@ below proves that it's a functor.
    proof :: forall a. AlgebraType0 m a
	  => Proof (AlgebraType m (m a)) (m a)
    -- |
    -- Proof that the forgetful functor from types @a@ satisfying
    -- @AgelbraType m a@ to @AlgebraType0 m a@ is well defined.
    forget :: forall a. AlgebraType  m a
	   => Proof (AlgebraType0 m a) (m a)

-- |
-- All types which satisfy @'FreeAlgebra'@ constraint are foldable.
--
-- prop> foldFree . returnFree == id
--
foldFree
    :: forall m a .
       ( FreeAlgebra  m
       , AlgebraType  m a
       )
    => m a
    -> a
foldFree ma = case forget @m @a of
    Proof Dict -> foldMapFree id ma

type instance AlgebraType0 [] a = ()
type instance AlgebraType  [] m = Monoid m
instance FreeAlgebra [] where
    returnFree a = [a]
    foldMapFree = foldMap
    proof  = Proof Dict
    forget = Proof Dict

The type class FreeAlgebra has many more instances, e.g. for semigroups, groups, idempotent semigroups (semi-lattices), abelian semigroups / monoids / groups, and there is even a version for functors, applicative functors and monads. For simplicity, in this post we will not touch the higher kinded types, but all of this works perfectly well for such data types too. You may ask what this type instance mean for monoids? We have two maps

returnFree @[] :: a -> [a]

and a bijective map

foldMapFree @[] :: forall m a. Monoid m => (a -> m) -> ([a] -> m)

given by Prelude.foldMap with inverse

unFoldMapFree
    :: FreeAlgebra m
    => (m a -> d)
    -> (a -> d)
unFoldMapFree f = f . returnFree

Note that foldMap (also foldMapFree) has some nice properties:

For each f :: Monoid m => a -> m the map foldMap f :: Monoid m => [a] -> m is a homomorphism of monoids, i.e.
```
foldMap f (as <> bs) = foldMap f as <> foldMap f bs
```
This is simply because foldMap maps the elements of as :: [a] to a list of type [m] and then folds them using monoid multiplication. Being a monoid homomorphism in this case just means that we can take two lists as :: [a] and bs :: [a] and foldMap over both of them and then multiply the results in m and we will get the same result as computing foldMap f (as ++ bs :: [a]). The result will be the same because monoids (and list concatenation) satisfy the associativity law.
When you will define an instance of FreeAlgebra you should check that this law is obeyed. Otherwise all the theory that we are uncovering here will fail.

You may think that it will fail to hold for non-associative monoids, since we used associativity here; but we used in two places at the same time: associativity of list concatenation and monoids, and this is crucial. For non associative monoids, the functor which will appear instead of a list will not obey the associativity law and it will not be required to prove that foldMapFree preserves non associative multiplication.
foldMap :: Monoid m => (a -> m) -> ([a] -> m) is natural in m which in turn means that
```
foldMap (f . g) = f . foldMap g
```
For any map g :: Monoid m => a -> m and any monoid homomorphisms: f :: (Monoid m, Monoid n) => m -> n.
foldMap :: Monoid m => (a -> m) -> ([a] -> m) is natural in d which means that
```
foldMap (g . h) = foldMap g . map h
```
For any map h :: b -> a and g :: Monoid m => a -> m.

The last two properties mean that foldMapFree (and foldMap) is a natural transformation of bifunctors from Hom m to AlgHom m which we define below.

data Hom m a b where
    Hom :: (AlgebraType0 m a, AlgebraType0 m b)
         => (a -> b)
         -> Hom m a b

bimapHom :: forall m a' a b b'.
            ( AlgebraType0 m a'
            , AlgebraType0 m b'
            )
         => (a' -> a)
         -> (b  -> b')
         -> Hom m a b
         -> Hom m a' b'
bimapHom f g (Hom ab) = Hom (g . ab . f)

data AlgHom m a b where
    AlgHom :: ( AlgebraType  m a
              , AlgebraType  m b
              )
           => (a -> b)
           -> AlgHom m a b

unAlgHom :: AlgHom m a b -> a -> b
unAlgHom (AlgHom f) = f

bimapAlgHom :: forall m a' a b b'.
               ( AlgebraType  m a'
               , AlgebraType  m b'
               )
            => (a' -> a)
            -> (b  -> b')
            -> AlgHom m a b
            -> AlgHom m a' b'
bimapAlgHom f g (AlgHom ab) = AlgHom (g . ab . f)

Note that you could define (full sub-) categories of Hask using these bifunctors.

We can put all four properties (together with foldMapFree being a bijection), into single statement: foldMapFree is a natural isomorphism between Hom m and AlgHom m:

-- |
ψ :: forall m a d .
         ( FreeAlgebra  m
         , AlgebraType0 m a
         )
      => AlgHom m (m a) d
      -> Hom m a d
ψ (AlgHom f) = case forget @m @d of
    Proof Dict -> Hom $ unFoldMapFree f

with inverse

-- |
φ :: forall m a d .
        ( FreeAlgebra  m
        , AlgebraType  m d
        , AlgebraType0 m a
        )
     => Hom m a d
     -> AlgHom m (m a) d
φ (Hom f) = case proof @m @a of
    Proof Dict -> case forget @m @(m a) of
        Proof Dict -> AlgHom $ foldMapFree f

Such natural bijections arising for a pair of functors F and U are called adjoint functors. In case of monoids the functor F is simply the list functor: [] and it is the left adjoin (it appears in the left argument of AlgHom) to the forgetful functor from the category of monoids to Hask (it's on the right hand since of Hom m a d though in an invisible way, only because we are dropping a constraint).

Unit and counit of an adjunction

Every adjunction can be characterised by two maps called unit and counit. The unit is defined as

unit :: forall m a .
        ( FreeAlgebra  m
        , AlgebraType0 m a
        )
     => Hom m a (m a)
unit = case proof @m @a of
    Proof Dict -> case forget @m @(m a) of
        Proof Dict -> ψ (AlgHom id)

and

counit :: forall m d .
          ( FreeAlgebra  m
          , AlgebraType  m d
          )
       => AlgHom m (m d) d
counit = case forget @m @d of
    Proof Dict -> φ (Hom id)

Let us decipher these morphisms. Let's start with counit

counit = φ (Hom id)
       = AlgHom (foldMapFree id)
       = AlgHom foldFree

So this looks familiar! In case of monoids this is just the good old friend fold. The unit is even simpler:

unit = ψ (AlgHom id)
     = Hom (unFoldMapFree id)
     = Hom returnFree

In case of monoids the unit is just (:[]) :: a -> [a].

Monad associated with an adjunction

Every adjunction gives rise to a monad. The left adjoint functor followed by the right adjoint functor is an endofunctor and a monad. In our case the left adjoin functor is the list functor [] from the Hask category to the category of monoids in Hask, while the right adjoin is the functor that forgets the Monoid constraint. So the composition is simply the list endo-functor on Hask: (:[]) :: a -> [a] I am sure you know that list is a monad, and it's the same monad as one given by the (unAlgHom counit) @[] :: [[a]] = [a]. Note that the map unAlgHo counit = foldFree and it can be recasted to a monad's join:

-- |
-- @'FreeAlgebra'@ constraint implies @Monad@ constraint.
joinFree :: forall m a .
          ( FreeAlgebra  m
          , AlgebraType0 m a
          )
         => m (m a)
         -> m a
joinFree mma = case proof @m @a of
    Proof Dict -> foldFree mma

From a join you can get the bind operator in a standard way:

-- |
-- |
-- The monadic @'bind'@ operator.  @'returnFree'@ is the corresponding
-- @'return'@ for this monad.
bindFree :: forall m a b .
            ( FreeAlgebra  m
            , AlgebraType0 m a
            , AlgebraType0 m b
            )
         => m a
         -> (a -> m b)
         -> m b
bindFree ma f = case proof @m @b of
    Proof Dict -> foldMapFree f ma

Together with returnFree :: FreeAlgebra m => a -> m a we have a very general formula for constructing monads; actually any monad arise in this way: from a pair of adjoint functors; the counit morphism defines join and the unit defines return. Let us put this monad in a wrapper type, we are using GADTs to capture the FreeAlgebra m constraint.

-- |
-- The composition of @Free@ followed by @U@
data FreeMAlg (m :: * -> *) (a :: *) where
    FreeMAlg :: ( FreeAlgebra m, AlgebraType m a )
             => m a -> FreeMAlg m a

runFreeMAlg :: FreeMAlg m a -> m a
runFreeMAlg (FreeMAlg ma) = ma

-- |
-- @FreeMAlg@ is a functor in the category @Hom m@.
fmapF :: forall m a b .
         Hom m a b
      -> FreeMAlg m a
      -> FreeMAlg m b
fmapF (Hom fn) (FreeMAlg ma) = FreeMAlg $ fmapFree fn ma

-- |
-- unit of the @FreeMAlg@ monad (i.e. @return@ in Haskell)
returnF :: forall m a .
           ( FreeAlgebra  m
           , AlgebraType0 m a
           , AlgebraType0 m (FreeMAlg m a)
           )
        => Hom m a (FreeMAlg m a)
returnF = case unit :: Hom m a (m a) of Hom f -> Hom (FreeMAlg . f)

-- |
-- join of the @FreeMAlg@ monad
joinF :: forall  m a .
         ( FreeAlgebra  m
         , AlgebraType0 m a
         , AlgebraType0 m (FreeMAlg m a)
         , AlgebraType0 m (FreeMAlg m (FreeMAlg m a))
         )
      => Hom m (FreeMAlg m (FreeMAlg m a)) (FreeMAlg m a)
joinF = case proof @m @a of
    Proof Dict -> case forget @m @(m a) of
        Proof Dict ->
	    Hom $ \(FreeMAlg mma)
		-> FreeMAlg $ joinFree $ fmapFree runFreeMAlg mma

-- |
-- bind of the @'FreeMAlg'@ monad
bindF :: forall m a b .
         ( FreeAlgebra  m
         , AlgebraType0 m b
         )
      => FreeMAlg m a
      -> Hom m a (FreeMAlg m b)
      -> FreeMAlg m b
bindF (FreeMAlg ma) (Hom f) = case proof @m @a of
    Proof Dict -> case forget @m @(m a) of
        Proof Dict -> FreeMAlg $ ma `bindFree` (runFreeMAlg . f)

Algebras for a monad

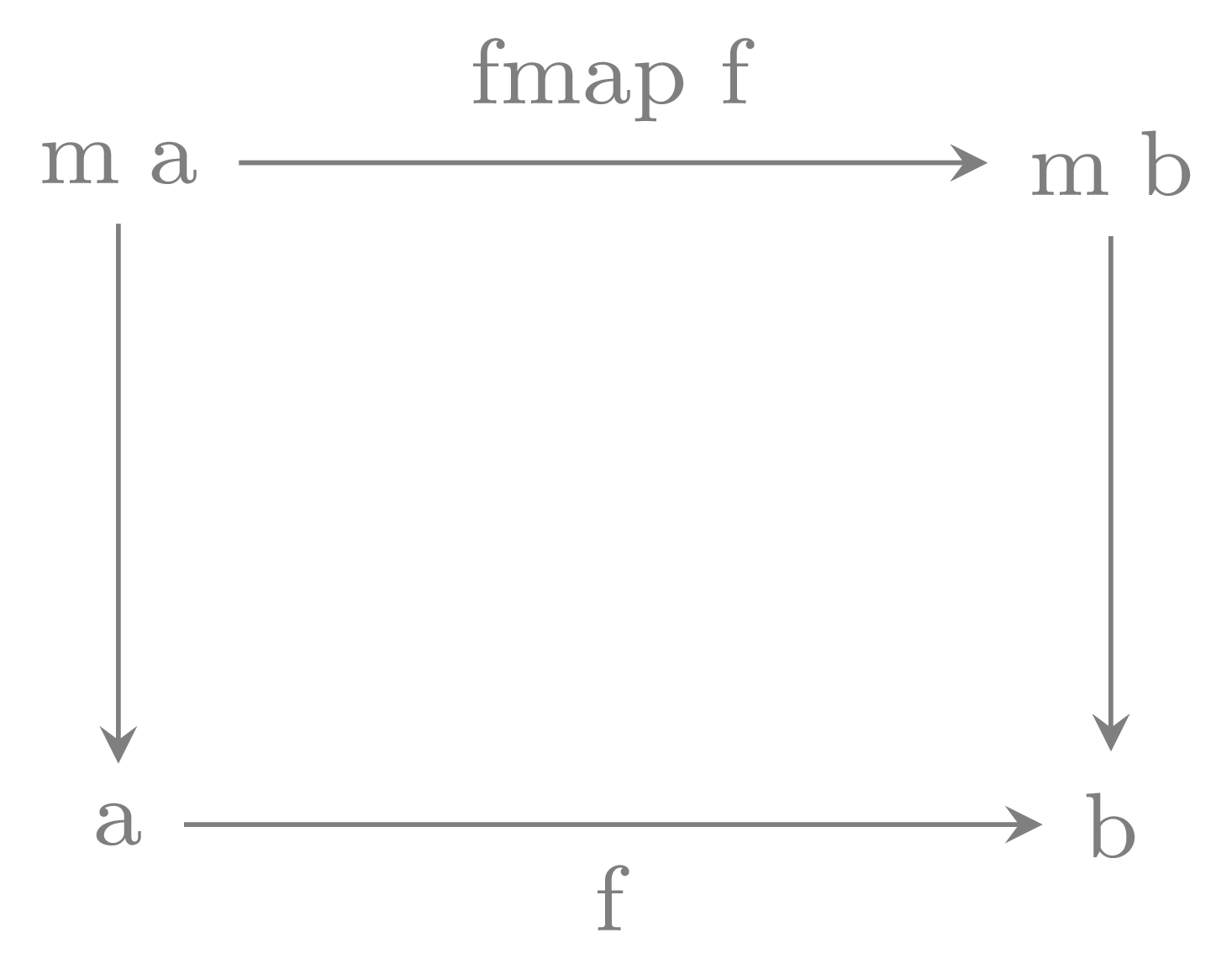
If m is a monad then an m-algebra is a map: m a -> a. m-algebras form a category where arrows are commutative squares.

The category of such algebras is called Eilenberg-Moore category, in was coined as a solution to the question: can every monad be defined through an adjunction? In Haskell this category will fit into a simple type class:

class MAlg m a where
    alg :: m a -> a

instance MAlg [] [a] where
    alg = concat

instance MAlg NonEmpty (NonEmpty a) where
    alg = NE.fromList . concatMap NE.toList

We can define MAlg instance for FreeMAlg:

instance ( FreeAlgebra m
         , AlgebraType0 m a
         , AlgebraType0 m (FreeMAlg m a)
         ) => MAlg m (FreeMAlg m a) where
    alg ma = case proof @m @a of
        Proof Dict -> FreeMAlg $ joinFree $ fmapFree runFreeMAlg ma

Note that this is an undecidable instance, since the constraints are not smaller than the instance head. It turns out that FreeMAlg m is a left adjoin functor to the forgetful functor $\mathrm{U_{MAlg}}$ from the category of m-algebras to $\mathrm{Hask}$ which sends an m-algebra f :: m a -> a to a. This is simply because we can write FreeAlgebra instance for this type. Well, not quite, only because Haskell computes types families in a lazy way, but we can define all the morphisms we need (we leave checking all the necessary properties though to the curious reader):

returnFreeMAlg
    :: FreeAlgebra m
    => a
    -> FreeMAlg m a
returnFreeMAlg = FreeMAlg . returnFree

foldMapFreeMAlg
    :: ( AlgebraType0 m a
       , AlgebraType0 m d
       , MAlg m d
       )
    => (a -> d)
    -> (FreeMAlg m a -> d)
foldMapFreeMAlg fn (FreeMAlg ma) = alg $ fmapFree fn ma

foldFreeMAlg
    :: ( AlgebraType0 m a
       , MAlg m a
       ) 
    => FreeMAlg m a -> a
foldFreeMAlg = foldMapFreeMAlg id

We're kind of at the starting point of this post again. Since we have an instance of FreeAlgebra we can define an adjunction in the same way, but for the class MAlg. So we end up with the following picture:

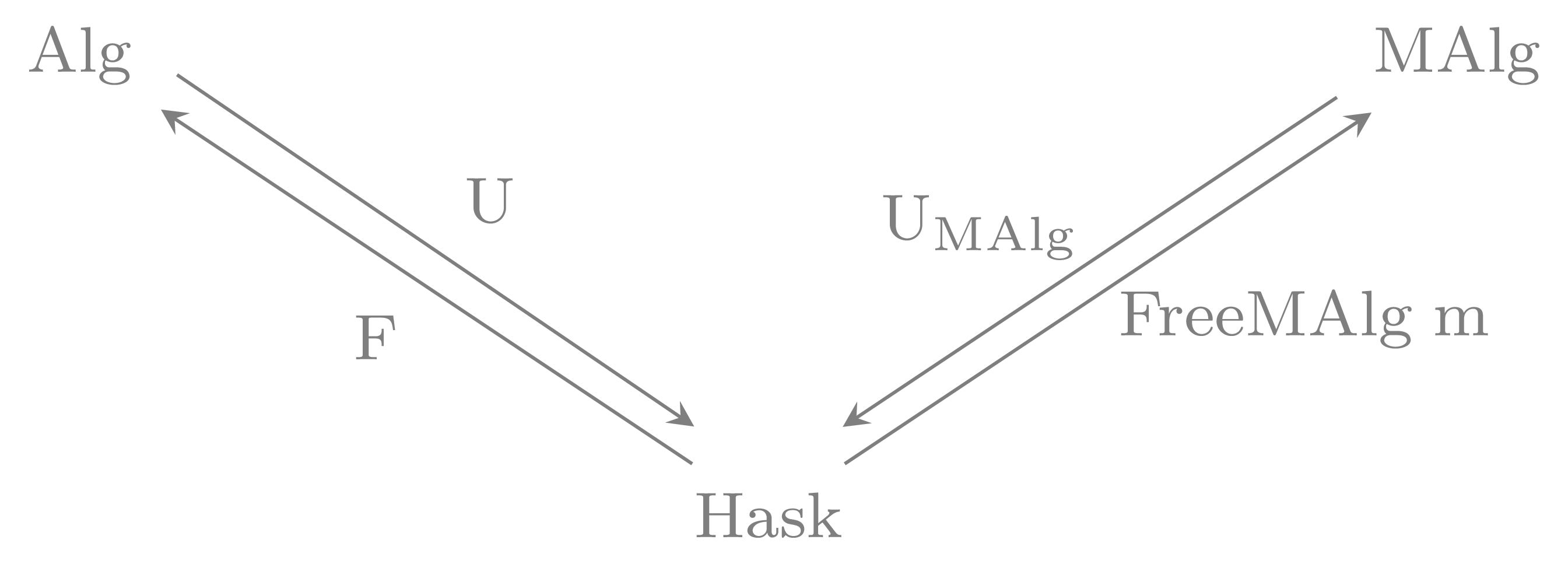
There is also a comparison functor which fills the diagram at the top. It is usually denoted by k and it takes an object in Alg (which is the category of monoids in our example case). k can be defined as follows:

k :: ( FreeAlgebra  m
     , AlgebraType  m a
     )
  => Proxy a
  -> (m a -> a)
k _ = foldFree

At the end we have a commutative diagram

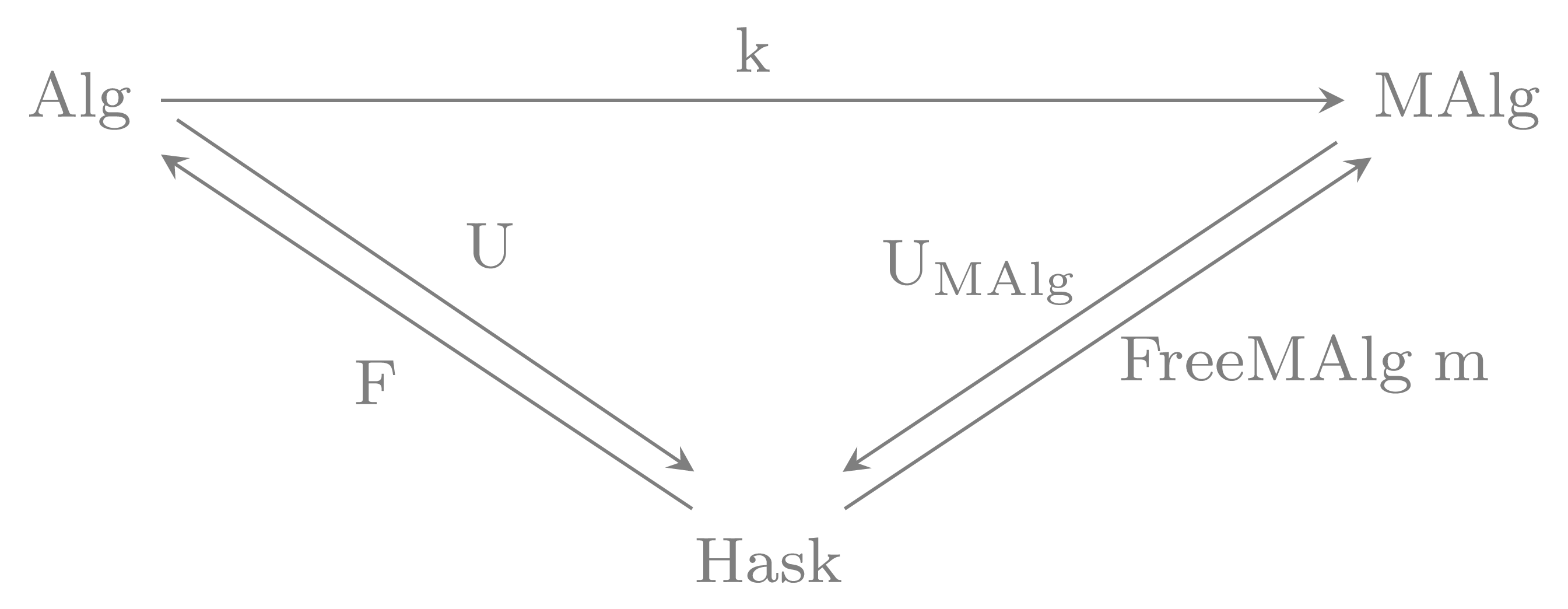
Monadicity

A right adjoin functor $\mathrm{U}$ is called monadic iff the comparison functor is an equivalence of categories. This means that the two categories Alg and MAlg have exactly the same categorical properties. It turns out that all algebraic theories which have free algebras (equivalently equational theories) are monadic. This includes the categories of semigroups, monoids, groups, etc are all monadic, but also the categories of functors, applicative functors and monads on Hask are monadic too. From technical point of view, maybe the most important fact is that the free monad encodes algebraic operations that the initial category was using. So in out example, we should be able to define <> and mempty only using the list monad. And it's quite trivial:

-- |
-- @'mempty'@ deduced from @FreeMAlg []@ @MAlg@ instance.
k_inv_monoid_mempty :: MAlg [] a => a
k_inv_monoid_mempty = foldFreeAlg (FreeMAlg [])

-- |
-- @'mappend'@ deduced from @FreeMAlg []@ @MAlg@ instance.
k_inv_monoid_mappend :: MAlg [] a => a -> a -> a
k_inv_monoid_mappend a b = foldFreeAlg (FreeMAlg [a, b])

-- |
-- @'<>'@ deduced from @FreeMAlg NonEmpty@ @MAAlg@ instance.
k_inv_semigroup_append :: MAlg NonEmpty a => a -> a -> a
k_inv_semigroup_append a b = foldFreeAlg (FreeMAlg (a :| [b]))

k_inv_pointed :: MAlg Maybe a => a
k_inv_pointed = foldFreeAlg (FreeMAlg Nothing)

-- |
-- @'invert'@ deduced from @FreeMAlg FreeGroup@ @MAlg@ instance.
k_inv_group_invert :: (MAlg FreeGroup a, Eq a) => a -> a
k_inv_group_invert a
    = foldFreeAlg (FreeMAlg (FreeGroup.fromList [Left a]))

-- |
-- @'act'@ deduced from @FreeMAlg FreeMSet@ @MAlg@ instance.
k_inv_act :: (MAlg (FreeMSet m) a, Monoid m) => m -> a -> a
k_inv_act m a = foldFreeAlg $ FreeMAlg $ FreeMSet (m, a)

A reference for free group: newtype FreeGroup a = FreeGroup [Either a a].

Laws

There is one more interesting thing here. Not only the operations are deduced from FreeMAlg m, but also the laws. For example, we use FreeMAlg [] for monoids and it encodes both associativity of the multiplication and unit law for mempty and this is simply cerried by the free monoid [a]. The same will hold for any other free algebra and thus by the monad FreeAlgebra m => m. This is just because the free algebra carries all the laws of the category of given algebra types (monoids / semigroups / lattices, ...) and no other equality is built in.

Final remarks

A working example on which this post is based is published on github. This monadicity works well for higher kinded algebras, e.g. functors, applicative functors or monads. The changes that one needs to make are really minimal: use FreeAlgebra1 type class of FreeAlgebra. Please check the code.